Terminal points on unit circle

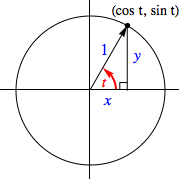
Let us refer to the circle centered at the origin of a Cartesian plane with radius one as the unit circle.

Given any real number $t$, there corresponds an angle of $t$ radians. Consider the point of intersection $P$ with coordinates $(x,y)$, of the terminal side of this angle (in standard position) with the unit circle.

Notice, if we drop a perpendicular from this point to the $x$-axis, we form a right triangle.

We have previously defined the cosine and sine functions for angles measuring between $0$ and $90^$ (i.e., between 0 and $\pi/2$ radians) to be the quotient of the adjacent side length to that of the hypotenuse, and the quotient of the opposite side length to the hypotenuse, respectively.

As the hypotenuse for our triangle has length one, it must be the case that when $0 \lt t \lt \pi/2$,

$$\cos t = x \quad \textrm < and >\quad \sin t = y$$

Seeing this, let us re-define the cosine and sine functions for any real value $t$ to be the $x$ and $y$ coordinates of the related and aforementioned point $P$.

Doing so provides a generalized version of these two functions -- one that preserves all of their previous output values for $0 \le t \le \pi/2$ while expanding their domains to now include all real values.

Let us take a moment and examine these two generalized functions before turning our attention to considering how to generalize the four remaining trigonometric functions.

Some Basic Properties of Sine and Cosine Functions

As mentioned previously, the domain of both the sine and cosine functions now consists of all real numbers
Note that both the $x$-coordinates and $y$-coordinates for points on the unit circle range from $-1$ to $1$, inclusive. Since each of these points is on the terminal side of some angle, the range of the sine and cosine functions must both be $[-1,1]$. That is to say, $$-1 \le \sin t \le 1 \quad \textrm < and >\quad -1 \le \cos t \le 1 \quad \textrm < for all >t$$
Since $x^2+y^2=1$ regardless of the angle $t$, the Pythagorean Identity below is preserved $$\cos^2 t + \sin^2 t = 1 \quad \textrm < for all >t$$
Since coterminal angles (angles whose measures differ by $2\pi n$ radians) have the same terminal side, and thus produce the same coordinates $x$ and $y$ for their respective points $P$, the following must be true, $$\left. \begin\sin(t \pm 2\pi n) &=& \sin t \\ \cos(t \pm 2\pi n) &=& \cos t \end \right\> \quad \textrm < where >n = 1, 2, 3, \ldots$$ When a function $f$ has the property that $f(x \pm kn) = f(x)$ for $n = 1,2,3,\ldots$, we say that function is periodic with period $k$. As such, the sine and cosine functions are periodic with a period of $2\pi$.
Since the aforementioned $P$ depends on the related angle $t$, let us define a function $P$ in the following manner: $$P(t) = (x,y) = (\cos t, \sin t)$$ Whether the values of $\cos t$ and $\sin t$ are positive or negative are determined the signs of the coordinates output by $P(t)$, which are themselves determined by the quadrant in which the terminal side of the angle in question falls, as shown on the right.
For some angles $t$, the values of $\sin t$ and $\cos t$ are easy to find by exploiting geometry, symmetry, and the occasional easily-found coordinates. This will be elaborated upon in the sections below.

Sine and Cosine Values for Integer Multiples of $\frac<\pi>$

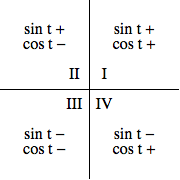
If an angle $\theta$ is an integer multiple of $\pi/2$ (i.e., $\theta = \frac$ for some integer $n$), then the terminal side of the angle in standard position lands on either the $x$-axis or $y$-axis. In this case, there are only four points of interest: $(1,0)$, $(0,1)$, $(-1,0)$, and $(0,-1)$. These points yield the following sine and cosine values:

$$\begin <|c|c|c|>t & \cos t & \sin t\\\hline 0 & 1 & 0 \\\hline \frac<\pi> & 0 & 1 \\\hline \pi & -1 & 0 \\\hline \frac<3\pi> & 0 & -1\\\hline \end$$

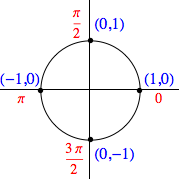
Of course, similar results are obtained for angles co-terminal to those above, as seen in the examples below: $$\cos \left( -\frac<3\pi> \right) = 1, \quad \sin(5\pi) = 0, \quad \cos(-6\pi) = 1, \quad \sin \left( -\frac<5\pi> \right) = -1$$

Sine and Cosine Values for Other Special Angles

Recall that we also already know the sine and cosine values for $30^$, $45^$ and $60^$ angles (i.e., $\pi/6$, $\pi/4$, and $\pi/3$ radians, respectively). We give these again below, expressing the angle measures in radians.

While one will find it useful to commit some of these values to memory, one need not remember all of them -- only the first two pairs. As the below graphic demonstrates, $\pi/6$ is $30^$ from the positive $x$-axis and $\pi/3$ is $30^$ from the positive $y$-axis. Consequently, the two triangles shown must be congruent. Thus, if one of the two marked points has coordinates $(x,y)$, the other must then have coordinates $(y,x)$. This in turn forces the values of the sine and cosine for $\pi/3$ to be the reverse of those for $\pi/6$ (as can be seen in the table above). Playing similar games with symmetry and triangles one can draw for various angles, we can expand our list of known sine and cosine values considerably, as the coordinates seen in the large graphic below suggest. One way to play these "symmetry games" is to realize that we can always express the values of the sine and cosine of angles whose terminal sides lie in quadrants II, III, and IV, in terms of the sine and cosine of a "reference angle" in the first quadrant, as follows:

Draw the given angle on a unit circle, noting the quadrant.
Find the associated reference angle, the angle between the terminal side of the given angle and the $x$-axis. The reference angle will necessarily be acute.
Find the sine and cosine of the reference angle, as needed -- these will have the same magnitudes (i.e., absolute value) as the sine and cosine of the given angle.
Adjust the signs of these values according to the quadrant of the given angle.

Generalizing the other Trigonometric Functions

In a manner consistent with right-triangle trigonometry, we define generalized versions of the tangent, secant, cotangent, and cosecant functions in terms of the sine and cosine functions as follows:

Note the restrictions on the domains of these other trigonometric functions. The values of $t$ excluded from their domains are those for which the denominators are equal to zero.

Since the other trigonometric functions are defined in terms of the sine and cosine, values of these other functions can easily be obtained for any $t$ for which the sine and cosine are known.